What I have learned from this ML project: Viterbi Algorithm is easier to code once you draw the flow.
Term 6 marks the official start of my business analytics track. It's the term of math, math and more math. As the prof usually says in class, "Machine learning is nothing but learning functions". This course was a good introduction on the models in machine learning as well as the project which gave me a greater insight on how to transform the mathematical formulas to code and to apply the code to predict.
In this project, we focused on building two simple NLP systems - a sentiment analysis system and phrase chunking system for Tweets. It was mainly designing a sequence labelling system.
We learned the Hidden Markov Model (HMM) in class which is a simple structured prediction model and we mainly used this in our project.
The HMM discussed in class is defined as the following equation:
$$p(x_1,..., x_n, y_1,...,y_n) = \prod_{i=1}^{n+1} q(y_i|y_{i-1}) • \prod_{i=1}^n e(x_i|y_i)$$
where $y_0$ = START , $y_{n+1}$ = STOP , $q$ are the transition probabilities and $e$ are the emission parameters.
To estimate the emission parameters, the number of times a tag y emitted a word x are counted and stored in emission_count_dict dictionary as a tuple (word, tag). y_count_dict stores the number of times a tag has appeared in the training file provided. For words that appear in the test set but not in the training set, they are known as unknown words and we replaced the word with #UNK# and smoothed the emission.
To estimate the transition parameters, the number of times a tag y appears and transition from previous tag to current tag are counted in the training set.
Using the estimated transition and emission parameters, the Viterbi Algorithm was implemented. Each node stores its parent node and the maximum probability to reach that node.
Second Order HMM
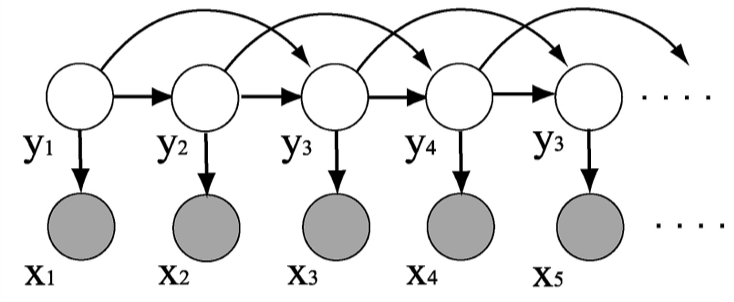
In second order HMM, the transition probabilities are changed to include the previous two tags while the emission parameters remains the same (as shown in the figure above).
To train model using second order Viterbi algorithm, instead of assign maximum score to each node, we assign maximum score to each [prev_tag, curr_tag] pair. In backtracking algorithm, we iterate through each [prev_tag, curr_tag] pair, and choose the pair which gives maximum score. The time complexity of this algorithm is $O(NT^3)$ where N is the number of words and T is the number of tags.
When multiplying probabilities, it is bound to reach values close to 0 since it gets smaller and smaller with every multiplication. A way to address numerical underflow issue is to sum the log of the probabilities instead of calculating the product of the probabilities.
Design Challenge
For our Design Challenge, we used Structured Perceptron to improve the accuracy of our English dataset and a better smoothing method - Good Turing Estimation for our French dataset.
Github Project Repo: https://github.com/rgan19/01.112_ML_Project
Modules I took this term: Optimisation, Machine Learning, The Analytics Edge
